![x = axt^3 + bxt^2 + cxt + d; y = ayt^3 + byt^2 + cyt + d; {t in [0,1]}](cubic.gif)
Calculus was always a possibility, of course. You want to compute the total effect of a complicated path; you break it down into small pieces and add them up, making sure that the pieces are small enough that the joints don't show. That's calculus. But I hadn't done any calculus since my freshman year of college, and I never really liked it much.
But I still had my old textbook, and it had tables of integrals. I figured one of them must be an answer I wanted.
What did I want? Take a cubic spline:
![x = axt^3 + bxt^2 + cxt + d; y = ayt^3 + byt^2 + cyt + d; {t in [0,1]}](cubic.gif)
I'm making the rules here, so what am I aiming for? This curve should have an effect on the vector field... an influence, making the field "more parallel" with the curve, with a strength that diminishes with distance. A longer curve should have a stronger influence.
I haven't solved anything. I still don't know what it means to be "more parallel" with a curve, nor what the distance to a curve is. (Distance to the center? To the nearest point? Neither is easy to figure.)
Well, a curve is an infinite array of points -- one corresponding to each real number t from zero to one. It's easy to figure out the distance to a point; and not much harder to figure out what it means to be parallel that point. (Or rather, parallel to the curve at that point.)
Of course, a program can't process an infinite array of points. What if I break it up into a finite array of short line segments? An approximation, of course. That's easy; you increment t in small steps. Now you have a chain of short line segments. You add up their effects... what are their effects?
Well, a line segment is an infinite array of points --
Oh dear.
But now the problem is easier. Cue the calculus. I can write down an expression for the effect of one point in the segment, and find the integral. That should give me the effect of the whole segment, in one swoop.
(Of course, I could have done an integral for the whole spline, too. But that would be harder. Laziness again, although perhaps not the best kind.)
My expression:

The sum of the inverse distances from point b to each point in the given line segment (a1 to a2)... In fact, I can simplify this to the problem where a1 is at the origin.
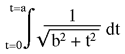
Off to the handy calculus textbook[3].
And lo, there's an integral for it.

But here's a twist. If I say that the influence falls off as the square of the distance, instead of proportionally, the integral is simpler:

I can live with that. After all, the laws of physics find it easier to work with inverse-square forces; why shouldn't I take a hint? Besides, if a point is inverse-square, then a bunch in a line should add up to inverse, which is what I wanted overall... A fuzzy thought, but it felt right.
I still needed a way to scatter strokes over the plane, randomly but at roughly constant spacing, according to a density map. My graphics textbook[4] had code for an error-diffusion dither, but it didn't work very well. At low densities, it tended to leave diagonal lines straggling down the page. That would be very visible in an ink-stroke field.
On the other hand, pgmtopbm[5]. the dithering tool I use in Unix, does a very nice job of scattering dots around a field -- even at low densities. So I went out to find some source code.
Turned out that it was error-diffusion dithering. I had been using a simple left-to-right, top-to-bottom path through the grid. You're supposed to use "boustrophedon" -- left-to-right on one row, right-to-left on the next. Works much better.
I also went out across the Web for some other formulas. A search for "graphics gems" turned up the archive of source code[6] for the old Graphics Gems books. That gave me the formula for the curvature of a spline at a given point. (Very useful when splitting the curve into small segments. You want to use smaller segments in the sections that are most sharply curved.) I also looked up the code for testing whether a given point is inside a polygon. (It seemed likely that I'd want some curves to only influence their interiors.)